59. 螺旋矩阵 II - 已题解语言：Java, Python, JavaScript, C#, Ruby, Go, C++ - 力扣题解最佳实践

59. 螺旋矩阵 II - 已用 Java, Python, JavaScript, C#, Ruby, Go, C++ 语言实现 - 力扣题解最佳实践 - 力扣人 [转发]

力扣链接：59. 螺旋矩阵 II，难度：中等。

给你一个正整数 n ，生成一个包含 1 到 n² 所有元素，且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。

示例 1:

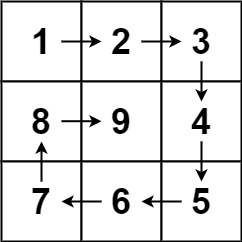
输入: n = 3

输出: [[1,2,3],[8,9,4],[7,6,5]]

示例 2:

输入: n = 1

输出: [[1]]

约束:

1 <= n <= 20

思路
上一题 下一题

本题的难点在于在二维数组中，如何获得当前位置的下一个位置。
可以写一个方法get_increment(i, j)，专门用于获得下一个位置与当前位置相比的变化量。

步骤

初始化 increments 和 increment_index:

increments = [(0, 1), (1, 0), (0, -1), (-1, 0)] # (i, j) right, down, left, up
increment_index = 0

核心逻辑:

while num <= n * n:
    matrix[i][j] = num
    num += 1

    increment = get_increment(i, j)
    i += increment[0]
    j += increment[1]

对于函数 get_increment(i, j)，它应该返回一对 [0, 1]。首先验证当前增量是否有效。如果无效，则使用下一个增量。

def get_increment(i, j):
    increment = increments[increment_index]
    i += increment[0]
    j += increment[1]

    if (
        i < 0 or i >= len(matrix) or
        j < 0 or j >= len(matrix) or
        matrix[i][j] is not None
    ): # 当前增量无效，使用下一个增量
        increment_index += 1
        increment_index %= len(self.increments)

    return increments[increment_index]

复杂度

时间复杂度

O(N * N)

空间复杂度

O(N * N)

Java #

class Solution {
    private int[][] matrix;
    private int[][] increments = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
    private int incrementIndex = 0;

    public int[][] generateMatrix(int n) {
        matrix = new int[n][n];
        var i = 0;
        var j = 0;
        var num = 1;

        while (num <= n * n) {
            matrix[i][j] = num;
            num++;

            var increment = getIncrement(i, j);
            i += increment[0];
            j += increment[1];
        }

        return matrix;
    }

    private int[] getIncrement(int i, int j) {
        var increment = increments[incrementIndex];
        i += increment[0];
        j += increment[1];

        if (
            i < 0 || i >= matrix.length || 
            j < 0 || j >= matrix.length || 
            matrix[i][j] > 0
        ) {
            incrementIndex += 1;
            incrementIndex %= increments.length;
        }

        return increments[incrementIndex];
    }
}

Python #

class Solution:
    def __init__(self):
        self.matrix = None
        self.increments = [(0, 1), (1, 0), (0, -1), (-1, 0)]
        self.increment_index = 0

    def generateMatrix(self, n: int) -> List[List[int]]:
        self.matrix = [[None] * n for _ in range(n)]
        i = 0
        j = 0
        num = 1

        while num <= n * n:
            self.matrix[i][j] = num
            num += 1

            increment = self.get_increment(i, j)
            i += increment[0]
            j += increment[1]

        return self.matrix

    def get_increment(self, i, j):
        increment = self.increments[self.increment_index]
        i += increment[0]
        j += increment[1]

        if (
            i < 0 or i >= len(self.matrix) or
            j < 0 or j >= len(self.matrix) or
            self.matrix[i][j]
        ):
            self.increment_index += 1
            self.increment_index %= len(self.increments)

        return self.increments[self.increment_index]

JavaScript #

let matrix
const increments = [[0, 1], [1, 0], [0, -1], [-1, 0]]
let incrementIndex

var generateMatrix = function (n) {
  matrix = Array(n).fill().map(() => Array(n).fill(0))
  incrementIndex = 0

  let i = 0
  let j = 0
  let num = 1

  while (num <= n * n) {
    matrix[i][j] = num
    num++

    const increment = getIncrement(i, j)
    i += increment[0]
    j += increment[1]
  }

  return matrix
};

function getIncrement(i, j) {
  const increment = increments[incrementIndex]
  i += increment[0]
  j += increment[1]

  if (
    i < 0 || i >= matrix.length ||
    j < 0 || j >= matrix.length ||
    matrix[i][j] > 0
  ) {
    incrementIndex += 1
    incrementIndex %= increments.length
  }

  return increments[incrementIndex]
}

C# #

public class Solution
{
    int[][] matrix;
    int[][] increments = { new[] {0, 1}, new[] {1, 0}, new[] {0, -1}, new[] {-1, 0} };
    int incrementIndex = 0;

    public int[][] GenerateMatrix(int n)
    {
        matrix = new int[n][];

        for (int k = 0; k < n; k++)
            matrix[k] = new int[n];

        int i = 0;
        int j = 0;
        int num = 1;

        while (num <= n * n)
        {
            matrix[i][j] = num;
            num++;

            int[] increment = getIncrement(i, j);
            i += increment[0];
            j += increment[1];
        }

        return matrix;
    }

    int[] getIncrement(int m, int n)
    {
        int[] increment = increments[incrementIndex];
        int i = m + increment[0];
        int j = n + increment[1];

        if (
            i < 0 || i >= matrix.GetLength(0) || 
            j < 0 || j >= matrix.GetLength(0) || 
            matrix[i][j] > 0
        )
        {
            incrementIndex += 1;
            incrementIndex %= increments.Length;
        }

        return increments[incrementIndex];
    }
}

Ruby #

def generate_matrix(n)
  @matrix = Array.new(n) { Array.new(n) }
  @increments = [[0, 1], [1, 0], [0, -1], [-1, 0]]
  @increment_index = 0

  i = 0
  j = 0
  num = 1

  while num <= n * n
    @matrix[i][j] = num
    num += 1

    increment = get_increment(i, j)
    i += increment[0]
    j += increment[1]
  end

  @matrix
end

private

def get_increment(i, j)
  increment = @increments[@increment_index]
  next_i = i + increment[0]
  next_j = j + increment[1]

  if next_i < 0 || next_i >= @matrix.size ||
    next_j < 0 || next_j >= @matrix.size ||
    @matrix[next_i][next_j]
    @increment_index += 1
    @increment_index %= @increments.size
  end

  @increments[@increment_index]
end

Go #

type spiralMatrix struct {
    matrix        [][]int
    increments    [][2]int
    incrementIndex int
}

func (sm *spiralMatrix) getIncrement(i, j int) [2]int {
    currentIncrement := sm.increments[sm.incrementIndex]
    nextI := i + currentIncrement[0]
    nextJ := j + currentIncrement[1]

    if nextI < 0 || nextI >= len(sm.matrix) || 
       nextJ < 0 || nextJ >= len(sm.matrix) || 
       sm.matrix[nextI][nextJ] != 0 {
        sm.incrementIndex = (sm.incrementIndex + 1) % len(sm.increments)
    }
    return sm.increments[sm.incrementIndex]
}

func generateMatrix(n int) [][]int {
    sm := &spiralMatrix{
        matrix: make([][]int, n),
        increments: [][2]int{{0, 1}, {1, 0}, {0, -1}, {-1, 0}},
        incrementIndex: 0,
    }

    for i := range sm.matrix {
        sm.matrix[i] = make([]int, n)
    }

    i, j, num := 0, 0, 1

    for num <= n * n {
        sm.matrix[i][j] = num
        num++

        increment := sm.getIncrement(i, j)
        i += increment[0]
        j += increment[1]
    }

    return sm.matrix
}

C++ #

class Solution {
public:
    vector<vector<int>> generateMatrix(int n) {
        matrix_ = vector<vector<int>>(n, vector<int>(n, 0));
        increments_ = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
        increment_index_ = 0;

        int i = 0;
        int j = 0;
        int num = 1;

        while (num <= n * n) {
            matrix_[i][j] = num;
            num++;

            vector<int> increment = getIncrement(i, j);
            i += increment[0];
            j += increment[1];
        }

        return matrix_;
    }

private:
    vector<vector<int>> matrix_;
    vector<vector<int>> increments_;
    int increment_index_;

    vector<int> getIncrement(int i, int j) {
        vector<int> increment = increments_[increment_index_];
        int next_i = i + increment[0];
        int next_j = j + increment[1];

        if (
            next_i < 0 || next_i >= matrix_.size() ||
            next_j < 0 || next_j >= matrix_.size() ||
            matrix_[next_i][next_j] > 0
        ) {
            increment_index_++;
            increment_index_ %= increments_.size();
        }

        return increments_[increment_index_];
    }
};

其它语言

欢迎贡献代码到我们的 GitHub 仓库，非常感谢！本题解位置在 59. 螺旋矩阵 II。

上一题下一题

游客

全部题解

Welcome !